Wstęp

W tym artykule przedstawimy zastosowania transformaty Fouriera w analizie szeregów czasowych. Wykorzystamy algorytm Fast Fourier Transform (Szybkiej Transformacji Fouriera), który jest dostępny w większości pakietów programistycznych i bibliotek statystycznych. Dla dociekliwego Czytelnika przedstawiono wizualizacje i przykłady kodu w Pythonie, które uzupełniają artykuł. Wszystkie one dostępne są w tym notatniku w Google Colab.

Choć temat transformaty Fouriera często wydaje się skomplikowany (głównie ze względu na skomplikowane na pierwszy rzut oka wzory), przekonamy się, że nawet podstawowe zastosowanie analizy Fouriera, przy użyciu ogólnodostępnych narzędzi, może dać dobre rezultaty.

Jak analizować dane pogodowe z wykorzystaniem analizy Fouriera

Załóżmy, że pracujemy na pewnych danych pogodowych.

data	temperatura
2008-01-01	0.49
2008-01-02	-2.82
2008-01-03	-5.75
2008-01-04	-7.37
2008-01-05	-6.10

W naszym zbiorze danych jest średnia dzienna temperatura dla pewnej lokalizacji.

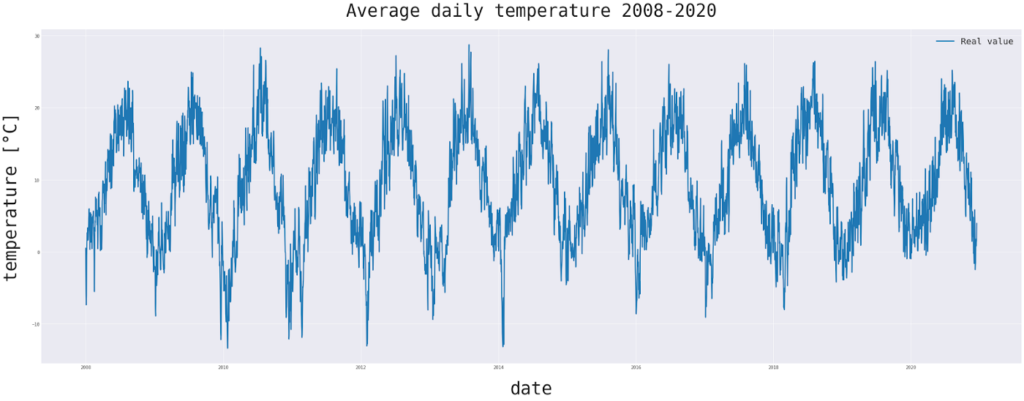
Jak widzimy, trend sinusoidalny panuje przez cały rok z pewną stałą częstotliwością. Jeśli możemy wiedzieć, jaka to jest częstotliwość, możemy zdekomponować sezonowość tego szeregu czasowego. Może to być przydatne do poprawy prognoz lub postępowania w przypadku brakujących pomiarów.

Analiza Fouriera

Naszym celem jest wzięcie tego jednozmiennego okresowego szeregu czasowego i zdekomponowanie go na prostsze funkcje okresowe.

Zgodnie z twierdzeniem sformułowanym przez Josepha Fouriera, każda funkcja okresowa, niezależnie od tego jak trywialna lub złożona, może być wyrażona jako kompozycja (połączenie) składników okresowych, znanych jako szereg Fouriera.

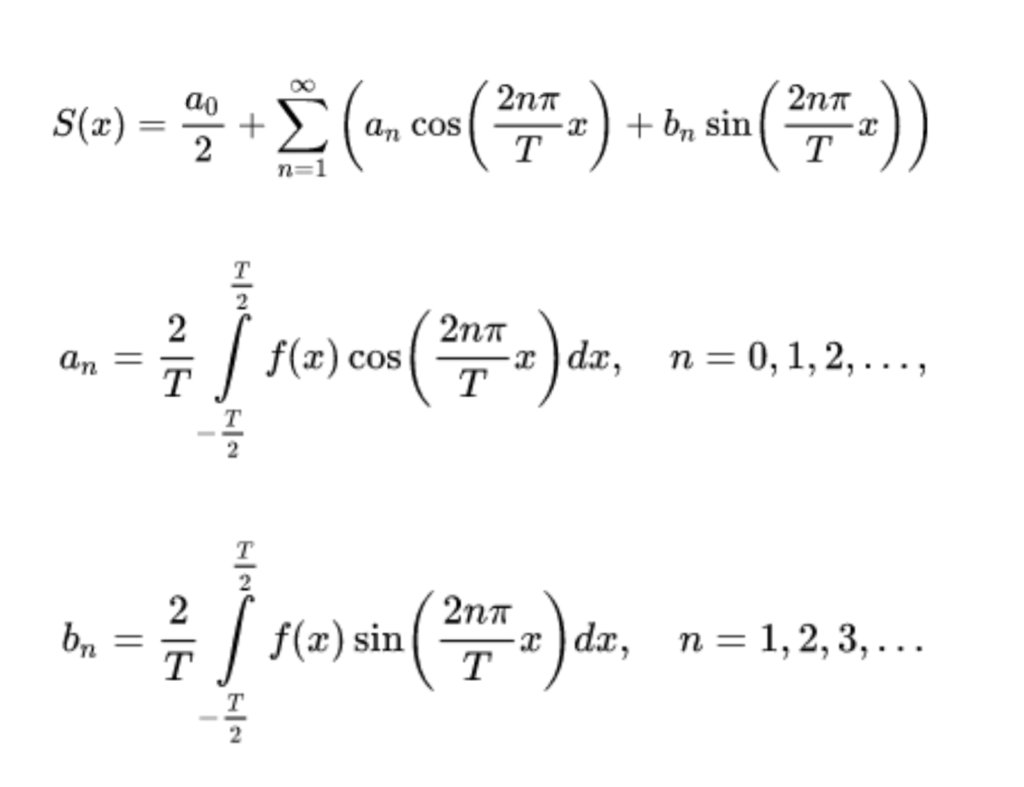
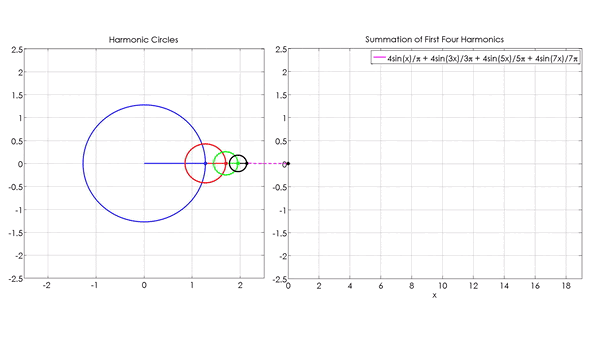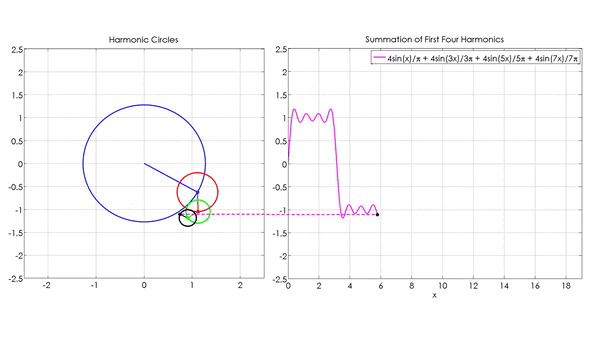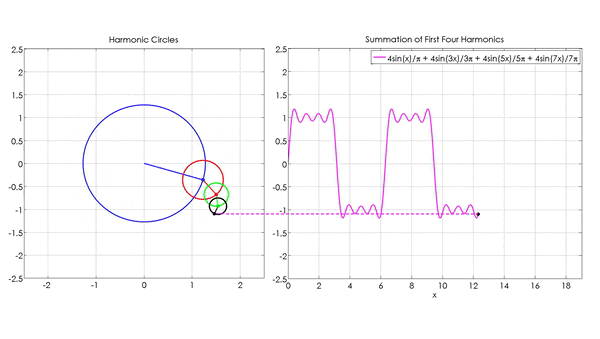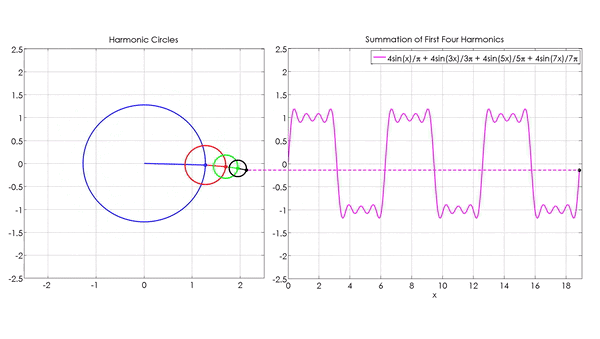
Wzory obliczające transformatę Fouriera wyglądają dosyć przerażająco. Jednakże idea za nimi stojąca jest bardzo prosta. Jak widzimy w animacji na górze tego artykułu, każda z funkcji sinus (lub cosinus) odpowiada jednemu okręgowi. Każda funkcja może zostać wyrażona za pomocą nieskończonej liczby takich okręgów.

Metoda wyrażania funkcji jako sumy sinusów i/lub cosinusów oraz odzyskiwania funkcji z tych składowych nosi nazwę analizy częstotliwościowej lub analizy Fouriera. Nie ma znaczenia, czy funkcja jest niesinusoidalna. Każdy okresowy szereg czasowy jest taką nieskończoną sumą składowych sinusoidalnych o współczynnikach.

Analiza Fouriera jest procesem uzyskiwania widma częstotliwości H(f) składających się na szereg czasowy h(t) i jest realizowana przez transformację Fouriera (FT). Analiza Fouriera przekształca szereg czasowy z jego pierwotnej dziedziny czasowej na reprezentację w dziedzinie częstotliwości i odwrotnie.

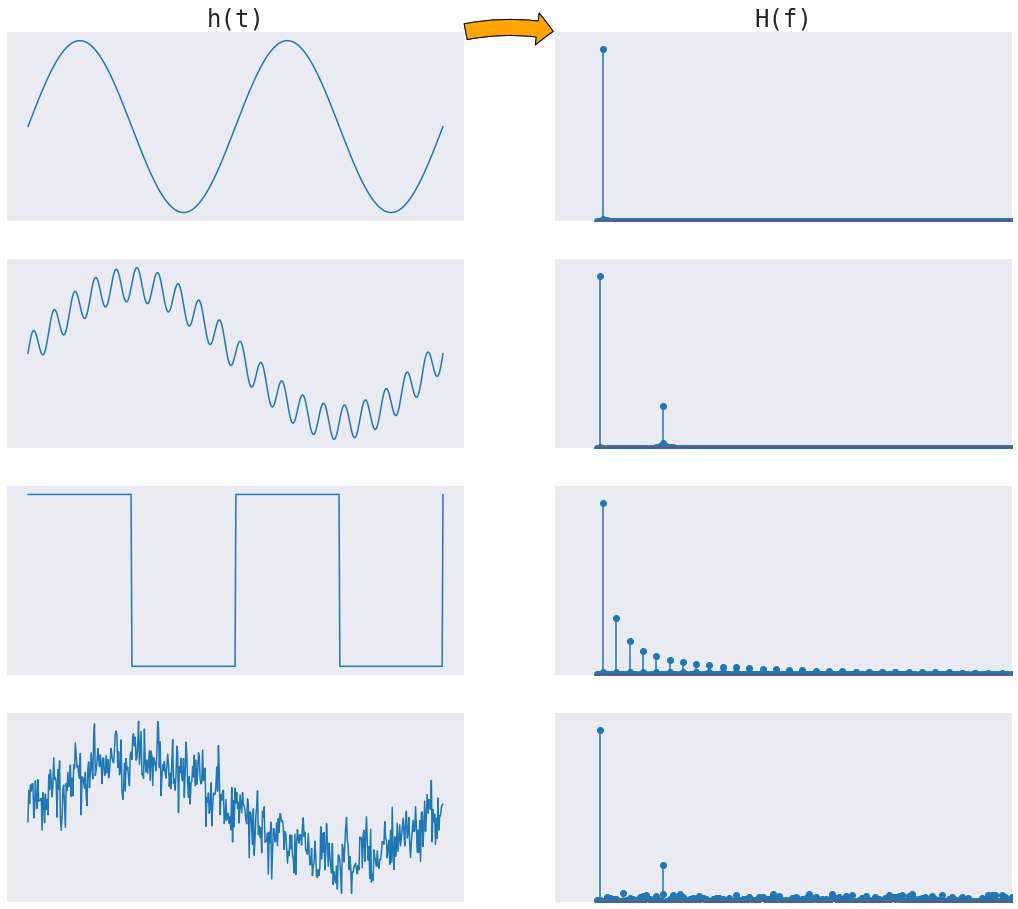
Mówiąc prościej, transformata Fouriera mierzy każdy możliwy cykl w szeregu czasowym i zwraca ogólny “przepis na cykl” (amplitudę, przesunięcie i prędkość obrotu dla każdego cyklu, który został znaleziony). Klasyczna transformata Fouriera jest dla funkcji ciągłych. Ponieważ nasze dane są dyskretne, użyjemy dyskretnego odpowiednika transformaty Fouriera.

Zastosujemy szybką transformatę Fouriera (ang. Fast Fourier Transform, FFT), algorytm obliczający dyskretną transformatę Fouriera (ang. Discrete Fourier Transform, DFT) szeregu czasowego lub jej odwrotność (ang. Inverse Discrete Fourier Transform, IDFT). DFT ma wiele zastosowań w fizyce, cyfrowym przetwarzaniu sygnałów i kompresji, np. w formatach MP3 i JPEG.

Jak wykryć sezonowość szeregów czasowych za pomocą szybkiej transformaty Fouriera?

W danych szeregu czasowego, sezonowość jest obecnością pewnych regularnych interwałów, które przewidywalnie powtarzają się w określonych ramach czasowych (np. tygodniowych, miesięcznych). Przykładem sezonowości może być powtarzająca się liczba samochodów przejeżdżających przez dane skrzyżowanie o określonych porach dnia. Dzięki takiej dekompozycji komponentów sezonowych z danych szeregu czasowego możemy poprawić dokładność prognozowania.

Istnieje wiele podejść do wykrywania sezonowości w szeregach czasowych, takich jak klasyczna dekompozycja i ekstrakcja sezonowa w metodach ARIMA (ang. Autoregressive integrated moving average, pol. Autoregresyjna zintegrowana średnia ruchoma). My natomiast użyjemy szybkiej transformacji Fouriera (FFT), aby znaleźć okres dominujących komponentów sezonowych w szeregu czasowym. Jako przykład można podać dane, które mają jeden silny efekt sezonowy i reszty. Intuicja podpowiada, że temperatura powinna mieć co najmniej roczny okres. Sprawdźmy to.

Procedura wyodrębniania sezonowości z szeregów czasowych jest prosta:

• Zastosuj transformatę Fouriera na zbiorze danych, aby uzyskać domenę częstotliwości.
• Posortuj malejąco domenę częstotliwości według współczynników.
• Weź najwyższy z nich i uzyskaj okresy dzieląc 1 przez częstotliwość.

nobs = len(data['temperature'])
temperature_ft = np.abs(rfft(data['temperature']))
temperature_freq = rfftfreq(nobs)

plt.figure(figsize=(10, 7))
plt.plot(temperature_freq[2:], temperature_ft[2: ])
annot_max(temperature_freq[2:], temperature_ft[2: ])
    
plt.xlabel('frequency (1/day)')
plt.show()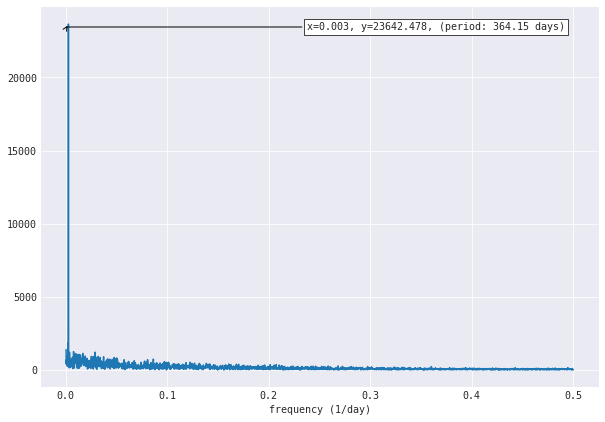

częstotliwość (1/dzień)	y	okres (dni)
0.0027	23642.48	364.15
0.0023	1837.26	430.36
0.0025	1528.34	394.50
0.0004	1396.18	2367.00
0.002	1296.69	338.14

Wynik był dość łatwy do przewidzenia. Temperatura powietrza zmienia się wraz z porami roku, więc największą wartość w widmie częstotliwości ma oczywiście okres ok. 365 dni. Wynik jest zgodny z powszechną wiedzą.

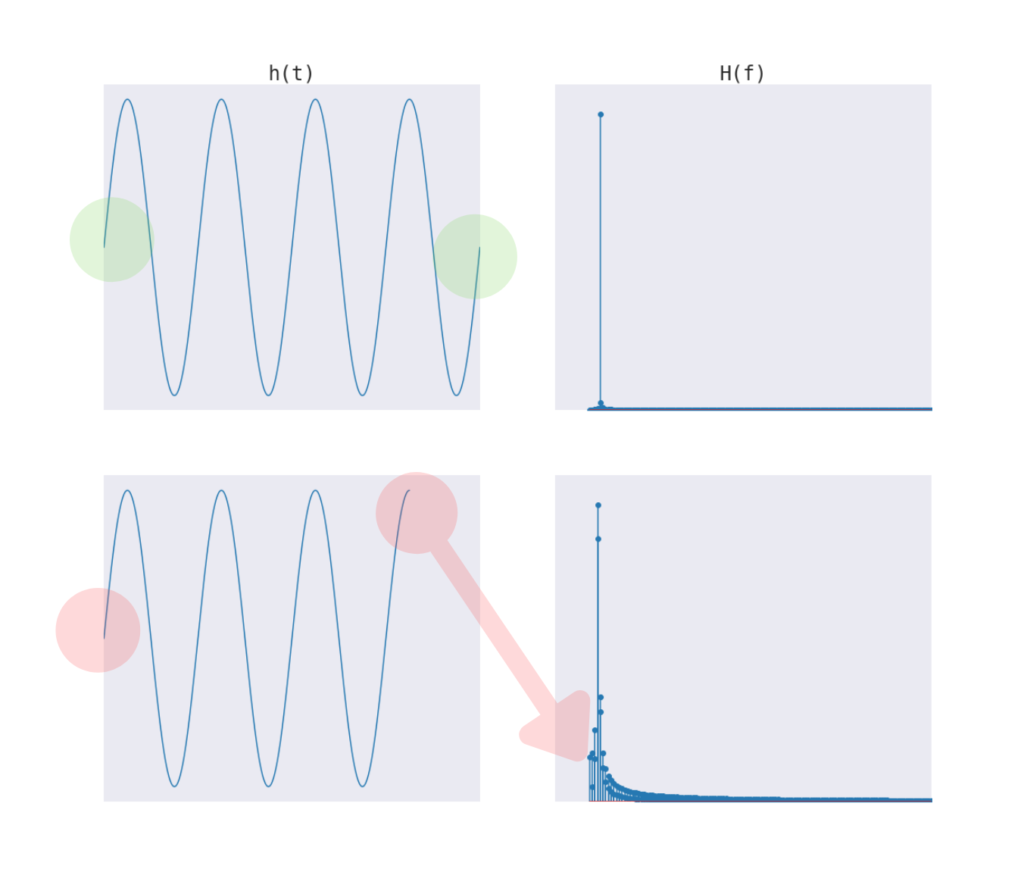
Przeciek widmowy Przeciek widmowy to zjawisko, kiedy po wykonaniu FFT na danych z niewielu okresów, pojawiają się nieistniejące wartości okresowe. Ponieważ w przypadku badanych przez nas tutaj danych mamy wartości z wielu pełnych okresów, raczej nie będziemy musieli się martwić o tego typu wyciek widma. Kiedy przeprowadzamy FFT na szeregu czasowym o skończonej długości, zakładamy, że dane powtarzają się do nieskończoności i łączą punkt końcowy z punktem początkowym. Ale kiedy istnieje nieciągłość, rozprzestrzenia się ona jako szczyt do otaczających częstotliwości.

Jak wygładzić szeregi czasowe za pomocą Inverse Fast Fourier Transform

Innym zastosowaniem FT jest wygładzanie danych z szeregów czasowych. Można o tym myśleć jak o:

• filtrowaniu dolnoprzepustowym, które można łatwo wykonać w celu usunięcia składowych o określonej częstotliwości ,
• filtrowaniu górnoprzepustowym, podczas gdy informacje zawierające składowe o niskiej częstotliwości są zachowywane. Dzięki temu pozbędziemy się niepotrzebnych, losowych wahań i fluktuacji z szeregu czasowego.

Można by zapytać, dlaczego nie zastosować metody średniej ruchomej lub wygładzania wykładniczego. Metody te nie wykorzystują obserwowanej okresowości w danych, Zatem np. jeśli w zbiorze danych występują luki, można je wypełnić jego estymacjami, dostosowując parametry IFT. Nie oznacza to, że musimy ograniczyć się tylko do funkcji o zauważalnej sezonowości.

Wahania dowolnej funkcji można wyciąć do pożądanego zakresu częstotliwości. Podobne podejście można zastosować do pozbycia się sezonowości w danych w celu zwiększenia stacjonarności szeregu czasowego. W takim przypadku należy zastosować filtr górnoprzepustowy.

Procedura jest prosta:

• Przenieś się do domeny częstotliwości. (Transformacja Fouriera)
• Usuń niepożądane częstotliwości.
• Przenieś się z powrotem do domeny czasu. (Odwrotna transformata Fouriera)

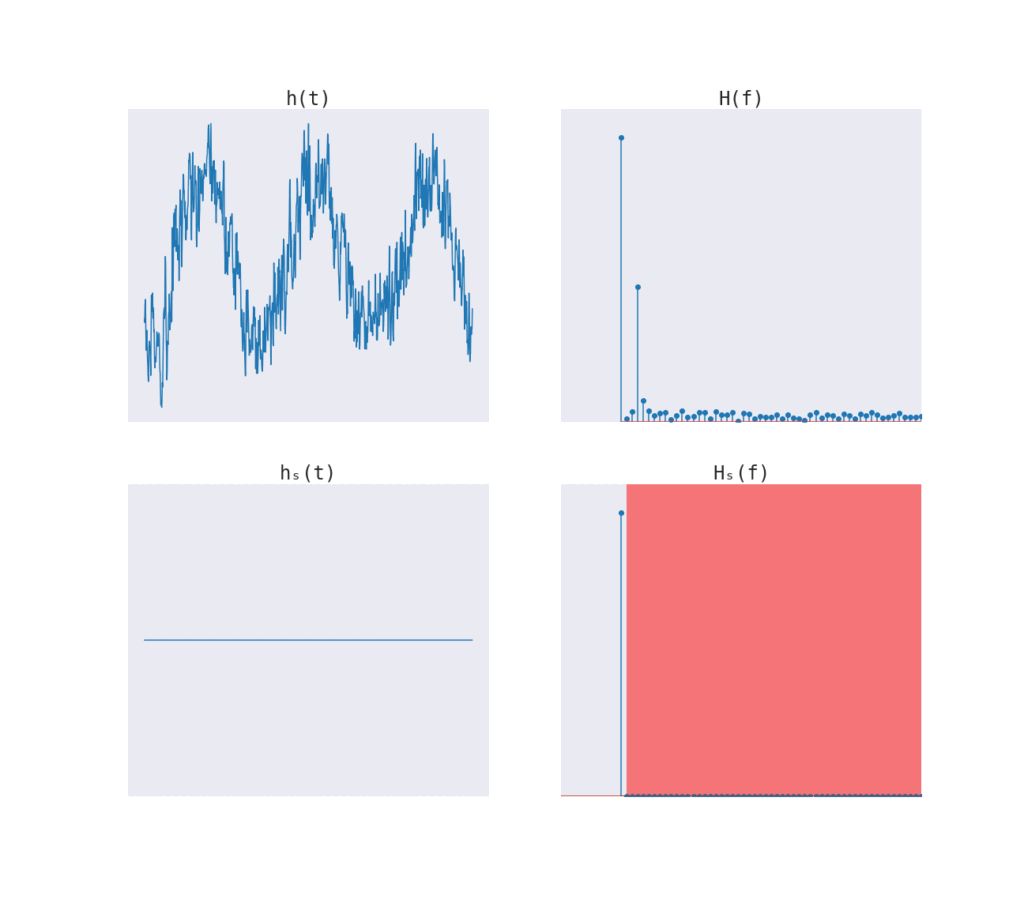
Zobaczmy jak taka procedura sprawdzi się dla naszych danych o temperaturze.

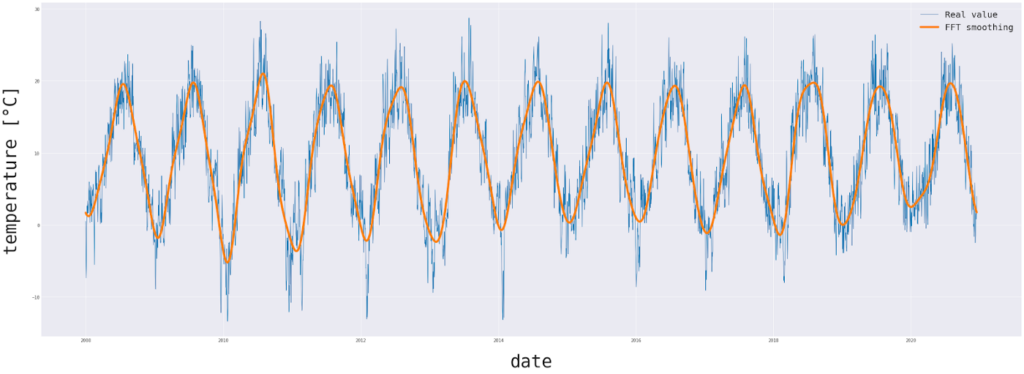
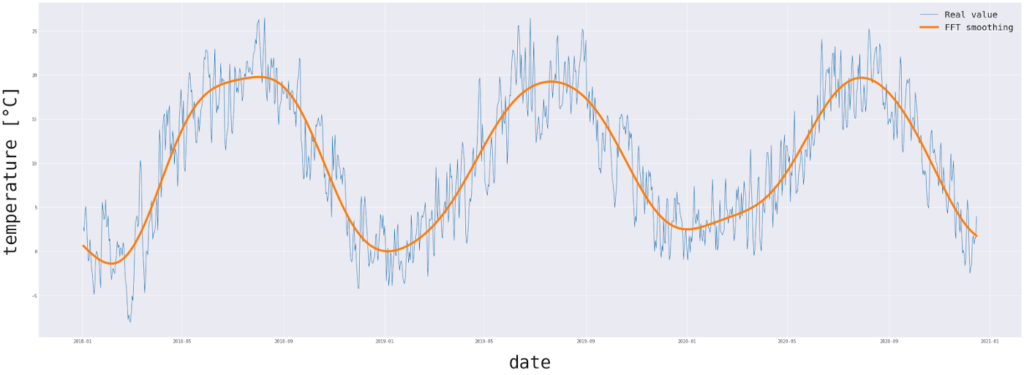
Podsumowanie

Jak widzimy analiza Fouriera może nam pomóc w uchwyceniu sezonowości i może być wykorzystana do dekompozycji danych szeregu czasowego. Poza swoją użytecznością, analiza Fouriera nie jest uniwersalnym narzędziem dla wszystkich problemów. FT jest świetny do szybkiego tworzenia modeli predykcyjnych dla danych z silną sezonowością. Specjalne zdarzenia w twoich danych, takie jak nieoczekiwane warunki pogodowe, nie byłyby przewidywane. Tak więc, możesz użyć analizy Fouriera, gdy:

• Zauważasz okresowość w danych
• Potrzebujesz szybkiego modelu prognozowania
• Chcesz wypełnić luki w danych